Chest pain in a young Woman - VA NR 8.12.19 - Annunzio
- bhofeld
- Aug 13, 2019
- 4 min read
Dr. Annunzio presented a case of a 33 yo F presenting with 1 day of stabbing chest pain, concurrently developing dyspnea and dizziness later in the day. She had DM1 and HTN, with a premature hx of CAD in her father. She was diagnosed with NSTEMI in the setting of sxs and precipitously increasing troponins with evoloving poor R wave progression. TTE showed large apical, septal, and anteroseptal wall hypokinesis. Cardiac cath demonstrated mid LAD 100% stenosis and pt underwent a drug eluding stent.
To begin our discussion of working up/ruling out ACS, we discussed Bayesian statistics as a tool for guiding diagnostic testing and empiric treatment.
Using Baye's Theorem and Nomograms to modify disease probabilities:
Intro: As physicians, estimating the probability that a patient has a certain disease is something we intrinsically do every day.
If a patient has a presumptive, but not definitive diagnosis, the likelihood of the patient having that diagnosis (disease probability) affects what we do next (further diagnostics, empiric treatment). What we do next is also influenced by the consequences of missing a diagnosis.
The more catastrophic the consequences of missing a diagnosis and/or not empirically treating a diagnosis, the lower your threshold should be for further workup of that diagnosis.

Nomogram: This is a very handy tool that we can use to modify the likelihood of someone having a disease based off of a test, symptom, Physical exam finding, criteria, etc. You start with a "Baseline Probability" of someone having a disease.
You then modify the probability by applying an Odds Ratio of a given test.
This modification produces a Post Test Probability.
This modification is important, because the Post Test Probability will influence:
1. whether we continue with diagnostics
2. what kind of diagnostics we order
3. whether we empirically treat a disease.
Each of these considerations has a specific threshold. If the threshold is met or exceeded, you should continue, and if it has not been met you should not.
Baye's Theorem (for our budding statistitians): P (A|B) = P (B|A) P(A) / P (B), Where:
P (A|B) = The probability that an event A occurs given an event B is true
P (B|A) = the probability that an event B occurs given an event A is true
P (A) = the probability that A is true (independently, by itself)
P (B) = the probability that B is true (independently, by itself)
Let's look at an example:
An otherwise healthy 30 YO male comes to your office withe vague cough and feeling a little "under the weather" for a week. At this point, what would you estimate is his disease probability for walking pneumonia?
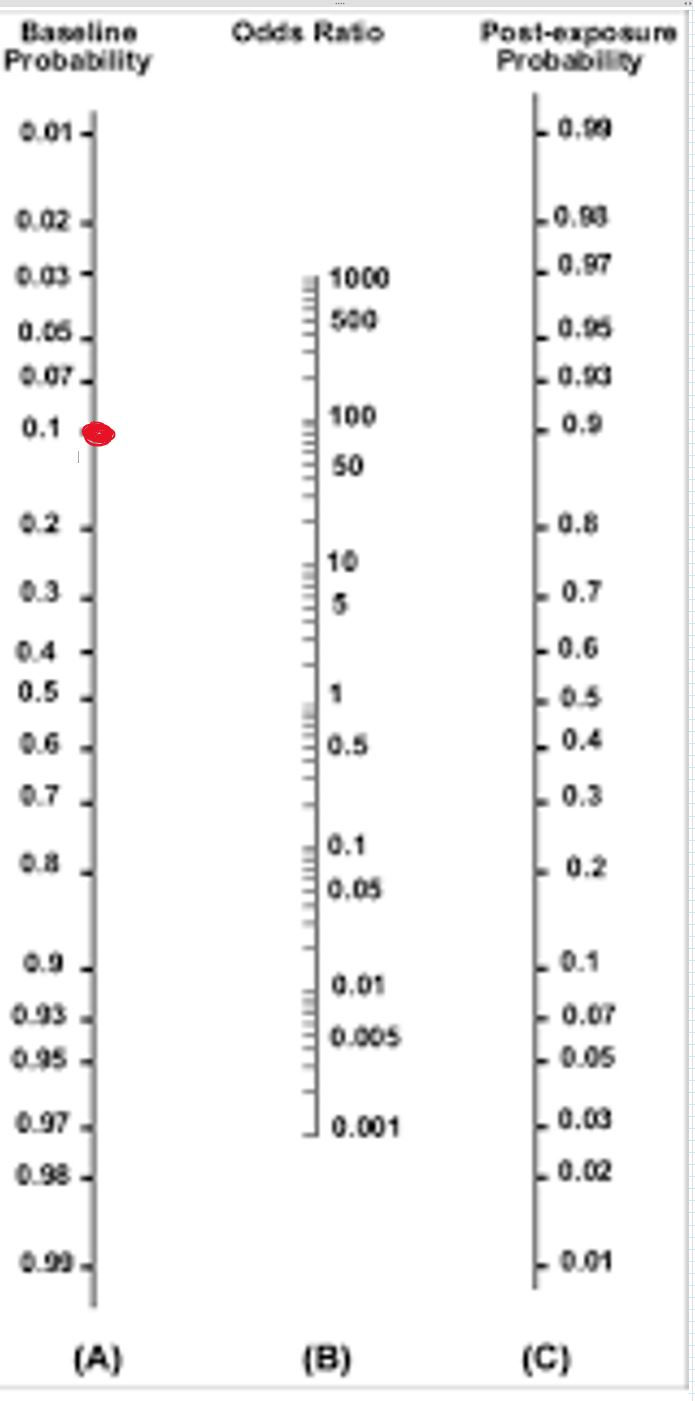
Let's estimate his pretest probability as 10%.
Remember that this probability is an estimate based off of what the provider knows about epidemiology, alternate diagnoses, and the limited information available.
Now we want to modify the disease probability in order to create a more accurate probability of whether this patient has the disease in question.
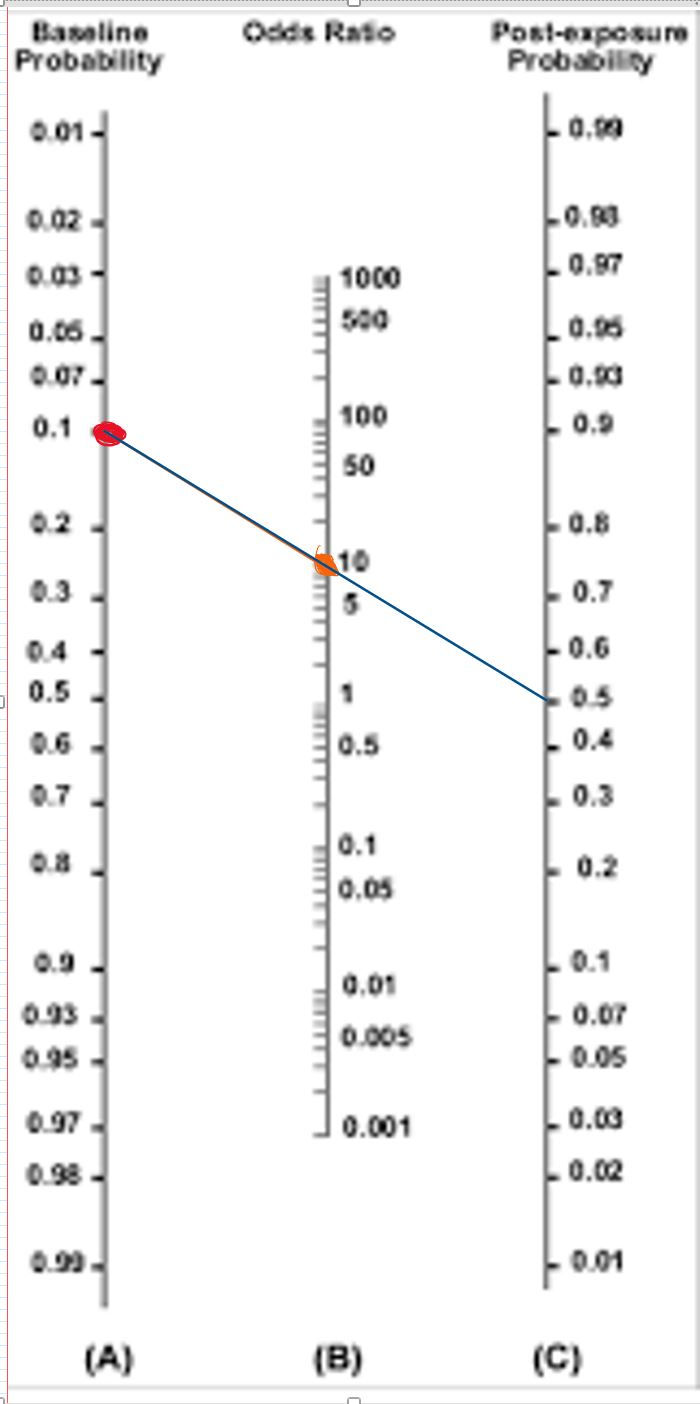
We can do this by instituting a test. In this case, let's use egophony from our physical exam. Let's say the positive likelihood ratio for this test is 10, and the negative likelihood ratio for this test is 0.9. On exam, this patient is positive for egophony.
Using the nomogram to the right, we 'modify' his disease probability by drawing a straight line through the baseline probability and likelihood ratio (similar to odds ratio) from the egophony test to determine his post-test probability. His post-test disease probability is now 0.5, or 50%.
Why are we doing this? Remember, we want to modify our disease probability to see if we can justify doing a further workup. In this example, performing a chest X-ray may be an important part of making the diagnosis of pneumonia in this patient. However, if this patient only has a 10% chance of having pneumonia, we may want to wait and observe this stable patient, as the more likely diagnosis is viral upper respiratory tract infection.
Let's say our threshold for ordering a chest X-ray in a suspected pneumonia is 20% for stable patients. In this case, applying the test of egophony has produced a change in management (we will now order the chest x-ray) which may lead to a more timely diagnosis and treatment!
Important points about Likelihood Ratios and Baye's Theorem
- A bias is created if you "pick and choose" which tests and likelihood ratios to apply
- you can combine tests' LRs by multiplying them together to get a combined likelihood ratio. This is essentially what scoring systems do (e.g. Modified Wells Criteria, TIMI score, etc).
- This should not supersede your clinical judgment, but rather help strengthen it. If there is a large discordance between your clinical gestalt and your post-test probability, either you are not being complete with the tests you are applying, or your gestalt is off (happens to all of us). The interplay between these two thought processes will make you a much stronger diagnostician.
For prior discussion on ACS Basics, please see:
Other ACS topics Discussed:
HEART Score
- A tool for undifferentiated chest pain in the urgent care setting.
- Identifies patients with having higher risk of MACE within the following 6 weeks
- Scoring System:

- Risk Stratification:
- Score 0-3: 0.9-1.7% risk of adverse cardiac event. Can be discharged
- Score 4-6: 12-16.6% risk of adverse cardiac event. Patients usually admitted
- Scores 7 or greater: 50-65% risk of adverse cardiac event. Candidates for early invasive measures
Urgent (<2 hrs) vs Early (w/ in 24 hr) Revascularization:
These characteristics portend increased likelihood of imminent cardiovascular event and should proceed for immediate cath:
●Hemodynamic instability
●Severe left ventricular diastolic dysfunction
●Recurrent or persistent rest angina despite intensive medical therapy
●New or worsening mitral regurgitation or new ventricular septal defect
●Sustained ventricular arrhythmias



Comments